假设检验

R语言
数据分析
各类假设检验相关方法的汇总
发布于

2024年8月10日

1 概念

假设检验是统计学中的一种方法，用于判断样本数据是否支持某个关于总体参数的假设。它的基本过程可以概括为以下几个步骤：

  • 提出假设：

    • 原假设（H0）：通常表示没有效应或没有差异的假设，是我们希望检验的初始假设。

    • 备择假设（H1）：表示存在效应或差异的假设。

  • 选择显著性水平（α）：

    • 这是一个预先设定的阈值，通常为0.05或0.01，用于决定何时拒绝原假设。

  • 选择检验统计量：

    • 根据数据的分布和样本大小，选择合适的检验统计量（如t检验、z检验、卡方检验等）。

  • 计算检验统计量：

    • 使用样本数据计算出检验统计量的值。

  • 确定拒绝域或p值：

    • 基于显著性水平和所选择的检验统计量，确定拒绝原假设的区域或计算p值（在原假设成立的情况下，观察到样本数据或更极端数据的概率）。

  • 作出决策：

    • 如果检验统计量落入拒绝域，或者p值小于显著性水平，就拒绝原假设；否则，未能拒绝原假设。

  • 结论：

    • 根据检验结果，给出对研究问题的结论，并进行相应的解释。

假设检验广泛应用于医学、社会科学、市场研究等领域，以帮助研究人员根据样本数据做出推断和决策。注意，假设检验的结果并不能证明原假设为真的，而只能提供足够的证据支持或反驳它。

本文汇总了各个情况下应当采取的假设检验 图 1

flowchart LR
  L0(假设检验) --> A1(单样本检验)
  A1 --> B11(正态总体)
  A1  --> B12(总体未知)
  B11 --> C11(均值检验)
  C11 --> D11(方差已知) --> E11(Z 检验)
  C11 --> D12(方差未知) --> E12(t 检验)
  B11 --> C12(方差检验) --> E13(卡方检验)
  B12 --> C13(均值检验) --> E14(Wilcoxon 秩和检验)
  B12 --> C14(方差检验) --> E15[无检验方法]
  L0(假设检验) --> A2(两样本检验)
  A2 --> B21(正态总体)
  A2  --> B22(总体未知)
  B21 --> C21(均值检验)
  C21 --> D21(方差已知) --> E21(Z 检验)
  C21 --> D22(方差未知但相等) --> E22(t 检验)
  C21 --> D23(方差未知且不等) --> E23(Welch t 检验)
  B21 --> C22(方差检验) --> E24(F 检验)
  C22 --> E27(Bartlett 检验)
  B22 --> C23(均值检验) --> E25(Wilcoxon 符号秩检验\nKruskal-Wallis 秩和检验)
  B22 --> C24(方差检验) --> E28(Ansari-Bradley 检验\nMood 检验\nFligner-Killeen 检验)
  L0(假设检验) --> A3(多样本检验)
  A3 --> B31(正态总体)
  B31 --> C31(均值检验) --> D31(方差相等) --> E31(F 检验)
  B31 --> C32(方差检验) --> E32(Hartley 检验\nBartlett 检验\n修正的 Bartlett 检验\nLevene 检验)
  C31--> D32(方差不等) --> E33(F 检验)
  A3 --> B33(总体未知)
  B33 --> C33(均值检验) --> E38(Kruskal-Wallis 秩和检验)
  B33 --> C34(方差检验) --> E39(Fligner-Killeen 检验)
  L0(假设检验) --> A4(配对样本检验)
  A4 --> B41(正态总体) --> C41(均值检验) --> E34(配对 t 检验)
  A4 --> B42(总体未知) --> C42(均值检验) --> E35(Wilcoxon 符号秩检验)
  L0(假设检验) --> A5(多重假设检验)
  A5 --> B51(多样本) --> E36(pairwise.t.test\npairwise.prop.test\npairwise.wilcox.test)
  A5 --> B52(Dunn 检验) --> E37(dunn.test)
图 1: 假设检验汇总

2 单样本检验

2.1 正态总体

随机变量 \(X\) 服从标准正态分布，它的概率分布函数如下：

\[ P(X \leq u)= \phi(u) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{u}\mathrm{e}^{-t^2/2}\mathrm{dt} \]

2.1.1 均值检验

2.1.1.1 方差已知

\[ \begin{aligned} \mathrm{I} \quad H_0: \mu - \mu_0 \leq 0 \quad vs. \quad H_1: \mu - \mu_0 > 0 \\ \mathrm{II} \quad H_0: \mu - \mu_0 \geq 0 \quad vs. \quad H_1: \mu - \mu_0 < 0 \\ \mathrm{III} \quad H_0: \mu - \mu_0 = 0 \quad vs. \quad H_1: \mu - \mu_0 \neq 0 \end{aligned} \]

设 \(x_1,\cdots,x_n\) 是来自总体 \(\mathcal{N}(\mu,\sigma^2)\) 的样本，样本均值和方差分别

\[\bar{x} = \frac{\sum_{i=1}^{n}x_i}{n}\]

\[s^2 = \frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2\]

根据中心极限定理 \(\bar{x} \sim \mathcal{N}(\mu,\sigma^2 / n)\) ，则检验统计量服从标准正态分布

\[ u = \frac{\bar{x} - \mu_0}{\sigma / \sqrt{n}} \]

假定 \(\mu_0 = 1\) 对于检验问题 I 拒绝域 \(\{u \geq u_{1-\alpha}\}\)

代码 
set.seed(1234)
n <- 20
# 随机生成样本
x <- rnorm(n, mean = 2.5, sd = 2)

# 计算检验统计量
u <- (mean(x) - 1) / (2 / sqrt(n))

# 计算临界值
critical_value <- qnorm(p = 1 - 0.05, mean = 0, sd = 1)

# 计算 p 值
p_value <- 1 - pnorm(q = u)

# 输出结果
list(u = u, critical_value = critical_value, p_value = p_value)
$u
[1] 2.233098

$critical_value
[1] 1.644854

$p_value
[1] 0.01277123

显著性水平（α）为0.05时，检验统计量2.233 大于 1.645, p值 0.0128 小于0.05

2.1.1.2 方差未知

在实际应用中，特别是样本较小的情况下（通常 n < 30），我们通常无法准确知道总体方差。这时，我们只能用样本方差（S²）来估计总体方差。利用样本方差进行估计会引入不确定性，因此需要一个更为宽容的分布来进行推断，因此也就诞生了\(t\)分布。\(t\) 分布比正态分布有更厚的尾部，这意味着它能更好地处理小样本带来的额外不确定性。当样本数量增加时，\(t\) 分布会逐渐趋近于正态分布。因此，在样本量较小的情况下，使用 t 分布可以更准确地反映抽样误差。

\[ \begin{aligned} \mathrm{I} \quad H_0: \mu - \mu_0 \leq 0 \quad vs. \quad H_1: \mu - \mu_0 > 0 \\ \mathrm{II} \quad H_0: \mu - \mu_0 \geq 0 \quad vs. \quad H_1: \mu - \mu_0 < 0 \\ \mathrm{III} \quad H_0: \mu - \mu_0 = 0 \quad vs. \quad H_1: \mu - \mu_0 \neq 0 \end{aligned} \]

考虑到

\[ \begin{aligned} & \frac{\bar{x} - \mu}{\sigma / \sqrt{n}} \sim \mathcal{N}(0,1) \\ & \frac{(n-1)s^2}{\sigma^2} \sim \chi^2(n-1) \\ & \mathsf{E}\{s^2\} = \sigma^2 \quad \mathsf{Var}\{s^2\} = \frac{2\sigma^4}{n-1} \end{aligned} \]

根据 t 分布的定义，检验统计量服从 t 分布，即 \(t \sim t(n-1)\)

\[ t = \frac{\bar{x} - \mu_0}{s/\sqrt{n}} \]

假定 \(\mu_0 = 1\) 对于检验问题 I ，拒绝域 \(\{t \geq t_{1-\alpha}(n-1)\}\)

代码 
mu0 <- 1
# 计算样本均值
sample_mean <- mean(x)

# 计算样本标准差
sample_sd <- sd(x)

# 计算 t 值
t_value <- (sample_mean - mu0) / (sample_sd / sqrt(n))

# 输出 t 值
cat("t 值:", t_value, "\n")
t 值: 2.202684
代码 
# 计算自由度
df <- n - 1

# 计算 p 值（单侧检验）
p_value <- 1 - pt(t_value, df)

# 输出 p 值
cat("p 值:", p_value, "\n")
p 值: 0.02008155
代码 
# 结果判断
alpha <- 0.05 # 显著性水平
if (p_value < alpha) {
  cat("拒绝原假设：均值显著大于", mu0, "\n")
} else {
  cat("无法拒绝原假设：均值与", mu0, "没有显著差异\n")
}
拒绝原假设：均值显著大于 1

R中内置了t.test函数，可以方便的进行多种t检验

代码 
# 单边t检验,备择假设大于
t.test(x, mu = mu0, alternative = "greater")

    One Sample t-test

data:  x
t = 2.2027, df = 19, p-value = 0.02008
alternative hypothesis: true mean is greater than 1
95 percent confidence interval:
 1.214703      Inf
sample estimates:
mean of x 
 1.998672
代码 
# 单边t检验,备择假设小于
t.test(x, mu = mu0, alternative = "less")

    One Sample t-test

data:  x
t = 2.2027, df = 19, p-value = 0.9799
alternative hypothesis: true mean is less than 1
95 percent confidence interval:
     -Inf 2.782641
sample estimates:
mean of x 
 1.998672
代码 
# 双边检验，
t.test(x, mu = mu0, alternative = "two.sided")

    One Sample t-test

data:  x
t = 2.2027, df = 19, p-value = 0.04016
alternative hypothesis: true mean is not equal to 1
95 percent confidence interval:
 1.049719 2.947625
sample estimates:
mean of x 
 1.998672
表 1
0.75 0.8 0.9 0.95 0.975 0.99 0.995 0.999
1 1.0000 1.3764 3.0777 6.3138 12.7062 31.8205 63.6567 318.3088
2 0.8165 1.0607 1.8856 2.9200 4.3027 6.9646 9.9248 22.3271
3 0.7649 0.9785 1.6377 2.3534 3.1824 4.5407 5.8409 10.2145
4 0.7407 0.9410 1.5332 2.1318 2.7764 3.7469 4.6041 7.1732
5 0.7267 0.9195 1.4759 2.0150 2.5706 3.3649 4.0321 5.8934
6 0.7176 0.9057 1.4398 1.9432 2.4469 3.1427 3.7074 5.2076
7 0.7111 0.8960 1.4149 1.8946 2.3646 2.9980 3.4995 4.7853
8 0.7064 0.8889 1.3968 1.8595 2.3060 2.8965 3.3554 4.5008
9 0.7027 0.8834 1.3830 1.8331 2.2622 2.8214 3.2498 4.2968
10 0.6998 0.8791 1.3722 1.8125 2.2281 2.7638 3.1693 4.1437

2.1.2 方差检验

方差检验是统计学中用于比较两个或多个样本或群体之间的方差是否相等的一种方法。方差检验主要用于确定不同组数据的离散程度是否存在显著差异，从而影响后续的统计分析和假设检验。

卡方检验 \(\chi^2\) 检验统计量服从卡方分布。

\[ \begin{aligned} \mathrm{I} \quad H_0: \sigma^2 - \sigma^2_0 \leq 0 \quad vs. \quad H_1: \sigma^2 - \sigma^2_0 > 0 \\ \mathrm{II} \quad H_0: \sigma^2 - \sigma^2_0 \geq 0 \quad vs. \quad H_1: \sigma^2 - \sigma^2_0 < 0 \\ \mathrm{III} \quad H_0: \sigma^2 - \sigma^2_0 = 0 \quad vs. \quad H_1: \sigma^2 - \sigma^2_0 \neq 0 \end{aligned} \]

一般假定均值 \(\mu\) 是未知的。检验统计量服从卡方分布 \(\chi^2(n-1)\)

\[ \chi^2 = \frac{(n-1)s^2}{\sigma^2_0} \]

设 \(\sigma^2_0 = 1.5^2\) ，考虑检验问题 I

代码 
# 生成样本数据
set.seed(123)

# 计算样本方差
sample_variance <- var(x)

# 设置待检验的方差（假设值）
hypothesized_variance <- 1.5^2 # 方差的假设值

# 进行卡方检验
n <- length(x)
chi_square_statistic <- (n - 1) * sample_variance / hypothesized_variance
p_value <- 1 - pchisq(chi_square_statistic, df = n - 1)

# 输出结果
cat("卡方统计量:", chi_square_statistic, "\n")
卡方统计量: 34.717
代码 
cat("p值:", p_value, "\n")
p值: 0.01510361
代码 
# 设定显著性水平，判断是否拒绝原假设
alpha <- 0.05
if (p_value < alpha) {
  cat("拒绝原假设，说明样本方差与假设方差存在显著差异。\n")
} else {
  cat("未能拒绝原假设，样本方差与假设方差不存在显著差异。\n")
}
拒绝原假设，说明样本方差与假设方差存在显著差异。
表 2: \(\chi^2\) 分布的分位数表
0.005 0.01 0.025 0.05 0.1 0.9 0.95 0.975 0.99 0.995
1 0.0000 0.0002 0.0010 0.0039 0.0158 2.7055 3.8415 5.0239 6.6349 7.8794
2 0.0100 0.0201 0.0506 0.1026 0.2107 4.6052 5.9915 7.3778 9.2103 10.5966
3 0.0717 0.1148 0.2158 0.3518 0.5844 6.2514 7.8147 9.3484 11.3449 12.8382
4 0.2070 0.2971 0.4844 0.7107 1.0636 7.7794 9.4877 11.1433 13.2767 14.8603
5 0.4117 0.5543 0.8312 1.1455 1.6103 9.2364 11.0705 12.8325 15.0863 16.7496
6 0.6757 0.8721 1.2373 1.6354 2.2041 10.6446 12.5916 14.4494 16.8119 18.5476
7 0.9893 1.2390 1.6899 2.1673 2.8331 12.0170 14.0671 16.0128 18.4753 20.2777
8 1.3444 1.6465 2.1797 2.7326 3.4895 13.3616 15.5073 17.5345 20.0902 21.9550
9 1.7349 2.0879 2.7004 3.3251 4.1682 14.6837 16.9190 19.0228 21.6660 23.5894
10 2.1559 2.5582 3.2470 3.9403 4.8652 15.9872 18.3070 20.4832 23.2093 25.1882

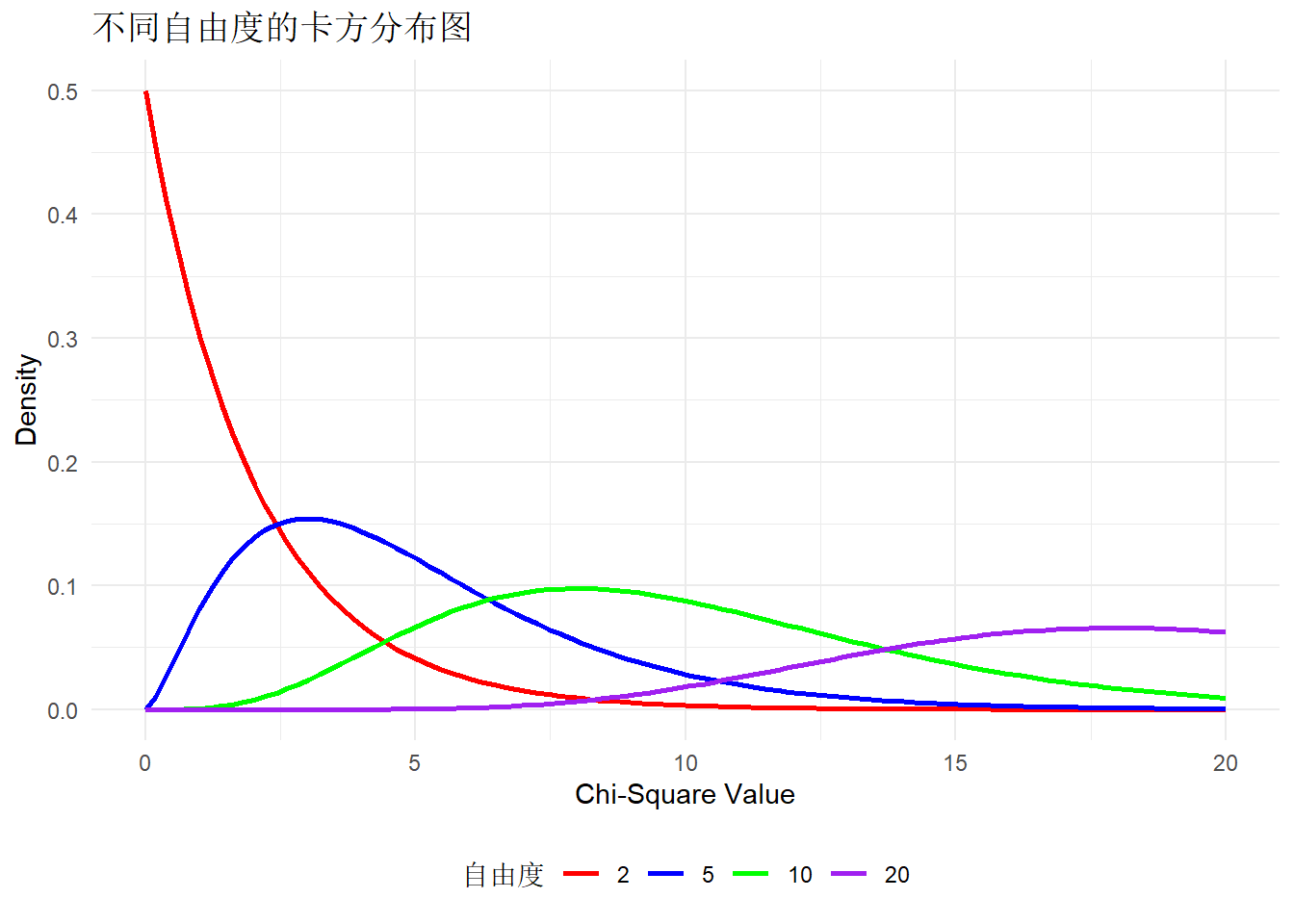
不同自由度的卡方分布图

图 2: \(\chi^2\) 分布图

卡方分布是由 n 个独立的标准正态随机变量的平方和得到的随机变量的分布。如果 \(Z_1,Z_2,...,Z_n\) 是标准正态分布的随机变量（均值为 0，方差为 1），则随机变量\[\chi^2 = Z_1^2 + Z_2^2+...+Z_n^2\]

服从自由度为 n 的卡方分布，记作 \(\chi^2(n)\)

特点:

  • 非负性：卡方分布的所有值都是非负的，因为正态变量的平方和不可能是负数。

  • 偏态性：卡方分布是右偏的，即大部分的值集中在较小的数值区域，但有较长的尾部。

  • 自由度：卡方分布的形状由自由度决定，自由度越大，分布越接近正态分布。

2.2 总体未知

2.2.1 均值检验

Wilcoxon符号秩检验：这是一种非参数统计检验，用于比较两个相关样本的中位数，当数据不符合正态分布时，Wilcoxon符号秩检验是一个替代t检验的有效方法。

代码 
wilcox.test(x = x, mu = mu0, alternative = "greater")

    Wilcoxon signed rank exact test

data:  x
V = 163, p-value = 0.01479
alternative hypothesis: true location is greater than 1
代码 
wilcox.test(x = x, mu = mu0, alternative = "less")

    Wilcoxon signed rank exact test

data:  x
V = 163, p-value = 0.9867
alternative hypothesis: true location is less than 1
代码 
wilcox.test(x = x, mu = mu0, alternative = "two.sided")

    Wilcoxon signed rank exact test

data:  x
V = 163, p-value = 0.02958
alternative hypothesis: true location is not equal to 1

2.3 两样本检验

2.3.1 正态总体

2.3.1.1 均值检验

两样本均值之差的检验

\[ \begin{aligned} \mathrm{I} \quad H_0: \mu_1 - \mu_2 \leq 0 \quad vs. \quad H_1: \mu_1 - \mu_2 > 0 \\ \mathrm{II} \quad H_0: \mu_1 - \mu_2 \geq 0 \quad vs. \quad H_1: \mu_1 - \mu_2 < 0 \\ \mathrm{III} \quad H_0: \mu_1 - \mu_2 = 0 \quad vs. \quad H_1: \mu_1 - \mu_2 \neq 0 \end{aligned} \]

2.3.1.1.1 方差已知

检验统计量如下：

\[ u = \frac{(\bar{x} - \bar{y}) - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma^2_1}{n1} + \frac{\sigma^2_2}{n2}} } \]

检验统计量服从标准正态分布 \(u \sim \mathcal{N}(0,1)\)，检验统计量 \(u\) 对应的样本值 \(u_0\)，检验的拒绝域和 \(P\) 值如下

\[ W_1 = \{u \geq u_{1 - \alpha} \}, \quad p_1 = 1 - \varPhi(u_0) \]

代码 
# 设置已知参数
mean1 <- 5 # 样本1的均值
mean2 <- 6 # 样本2的均值
n1 <- 30 # 样本1的大小
n2 <- 30 # 样本2的大小
sigma1 <- 1 # 样本1的标准差（已知总体标准差）
sigma2 <- 1 # 样本2的标准差（已知总体标准差）

# 计算Z检验统计量
z <- (mean1 - mean2) / sqrt((sigma1^2 / n1) + (sigma2^2 / n2))

# 输出Z值
print(paste("Z值:", z))
[1] "Z值: -3.87298334620742"
代码 
# 定义显著性水平
alpha <- 0.05

# 计算p值
p_value <- (1 - pnorm(abs(z))) # 单尾检验
# p_value <- 2 * (1 - pnorm(abs(z)))  # 双尾检验
# 输出p值
print(paste("p值:", p_value))
[1] "p值: 5.37555883647345e-05"
代码 
# 检验结果
if (p_value < alpha) {
  print("拒绝原假设，两个总体均值存在显著差异")
} else {
  print("未拒绝原假设，两个总体均值不存在显著差异")
}
[1] "拒绝原假设，两个总体均值存在显著差异"
2.3.1.1.2 方差未知但相等

设 \(x_1,\cdots,x_{n1}\) 是来自总体 \(\mathcal{N}(\mu_1,\sigma^2)\) 的样本，设 \(y_1,\cdots,y_{n2}\) 是来自总体 \(\mathcal{N}(\mu_2,\sigma^2)\) 的样本。

t 检验，检验统计量服从自由度为 \(n1 + n2 - 2\) 的 t 分布

\[ t = \frac{(\bar{x} -\bar{y})-(\mu_1 - \mu_2)}{s_0\sqrt{\frac{1}{n1} + \frac{1}{n2}}} \]

其中，

\[ \begin{aligned} & \bar{x} = \sum_{i=1}^{n1}x_i \quad \bar{y} = \sum_{i=1}^{n2}y_i \\ & s_0^2 = \frac{1}{n1 + n2 - 2}\big(\sum_{i=1}^{n1}(x_i - \bar{x})^2 + \sum_{i=1}^{n2}(y_i - \bar{y})^2\big) \end{aligned} \]

代码 
# 设置随机种子以便重现
set.seed(123)

# 生成两个正态分布样本
sample1 <- rnorm(30, mean = 5, sd = 1) # 样本1
sample2 <- rnorm(30, mean = 6, sd = 1) # 样本2


# 执行双样本t检验，并假设方差相等
t_test_result <- t.test(sample1, sample2, var.equal = TRUE)

# 输出检验结果
print(t_test_result)

    Two Sample t-test

data:  sample1 and sample2
t = -5.2098, df = 58, p-value = 2.616e-06
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -1.6962870 -0.7545972
sample estimates:
mean of x mean of y 
 4.952896  6.178338
2.3.1.1.3 方差未知且不等

两个样本的样本量不是很大，总体方差也未知，两样本均值之差的显著性检验，即著名的 Behrens-Fisher 问题，Welch 在 1938 年提出近似服从自由度为 \(l\) 的 t 分布。

Welch’s t-test（Welch检验）是一种用于比较两个独立样本均值的统计方法，特别是在以下情况下适用：

  • 方差不相等：与传统的t检验相比，Welch’s t-test不要求两个样本的方差相等。这使得它在处理现实数据时更加灵活和可靠。

  • 样本大小不同：该方法也能有效处理样本量不同的情况。

Welch’s t-test的基本原理是计算出样本均值的差异，并评估这一差异是否显著。其统计量依赖于样本均值、样本标准差和样本大小，并且使用了不同的自由度计算公式，以考虑方差的不等性。

设 \(x_1,\cdots,x_{n1}\) 是来自总体 \(\mathcal{N}(\mu_1,\sigma_1^2)\) 的 IID 样本，设 \(y_1,\cdots,y_{n2}\) 是来自总体 \(\mathcal{N}(\mu_2,\sigma_2^2)\) 的 IID 样本。

\[ T = \frac{(\bar{x} - \bar{y}) - (\mu_1 - \mu_2)}{\sqrt{\frac{s_x^2}{n1} + \frac{s_y^2}{n2}} } \]

其中，\(s_x^2\) 表示样本 x 的方差 \(s_x^2 = \frac{1}{n1-1}\sum_{i=1}^{n1}(x_i -\bar{x})^2\) ，\(s_y^2\) 表示样本 y 的方差 \(s_y^2 = \frac{1}{n2-1}\sum_{i=1}^{n2}(y_i -\bar{y})^2\) 。检验统计量 \(T\) 服从自由度为 \(l\) 的 t 分布。

\[ l = \frac{s_0^4}{ \frac{s_x^4}{n1^2(n1 - 1)} + \frac{s_y^4}{n2^2(n2-1)} } \]

其中， \(s_0^2 = s_x^2 / n1 + s_y^2/n2\)，\(l\) 通常不是整数，实际使用时，\(l\) 可取最近的整数。

在R语言中，通过设置t.test的参数var.equal = FALSE就可以进行Welch’s t-test

代码 
# 假设有两个样本
sample1 <- c(10.5, 12.3, 11.7, 14.2, 13.8)
sample2 <- c(8.9, 10.1, 9.5, 11.0, 8.7)

# 执行Welch's t-test
result <- t.test(sample1, sample2, var.equal = FALSE)

# 输出结果
print(result)

    Welch Two Sample t-test

data:  sample1 and sample2
t = 3.5789, df = 6.6526, p-value = 0.009792
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 0.9501803 4.7698197
sample estimates:
mean of x mean of y 
    12.50      9.64

2.3.1.2 方差检验

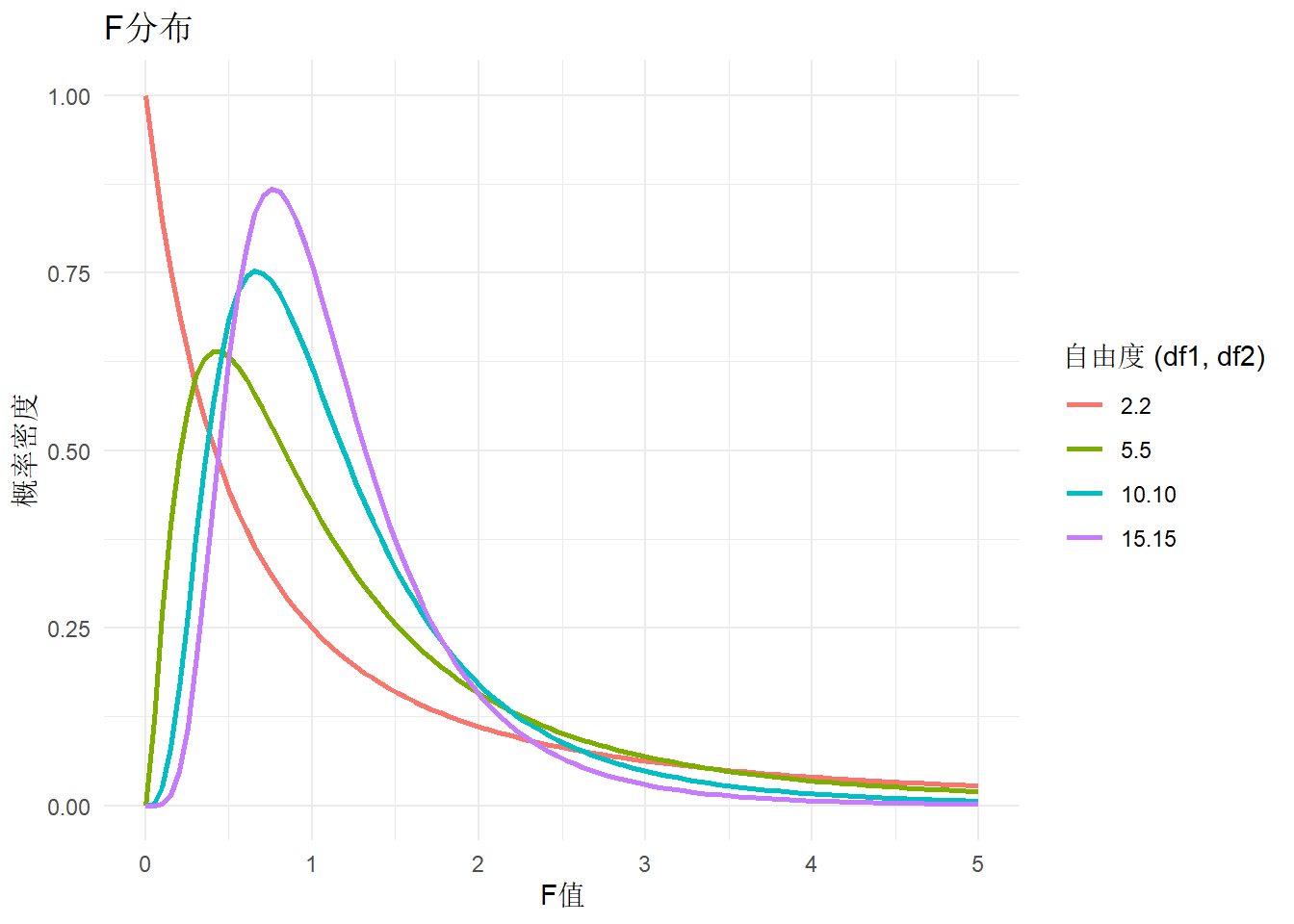
进行两样本正态总体方差检验可以使用var.test()函数。这个函数用于检验两个样本是否来自具有相同方差的正态总体。以下是使用var.test()函数的一个示例：

代码 
# 假设我们有两个样本数据集x和y
x <- c(10, 12, 14, 16, 18)
y <- c(9, 11, 13, 15, 17)

# 使用var.test()函数进行方差检验
result <- var.test(x, y)
result

    F test to compare two variances

data:  x and y
F = 1, num df = 4, denom df = 4, p-value = 1
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.1041175 9.6045299
sample estimates:
ratio of variances 
                 1

var.test()函数的输出将包括一个F统计量和相应的P值。F统计量的计算基于两个样本的方差比，如果P值小于常用的显著性水平（例如0.05），则我们拒绝原假设，认为两个样本的方差不相等。

如果需要对数据集进行更复杂的分析时，可以使用bartlett.test()函数，它是一种更加通用的方差齐性检验方法，支持多样本情况：

代码 
bartlett.test(Sepal.Length ~ Species, data = iris)

    Bartlett test of homogeneity of variances

data:  Sepal.Length by Species
Bartlett's K-squared = 16.006, df = 2, p-value = 0.0003345

2.3.2 总体未知

2.3.2.1 均值检验

采用wilcox.test, wilcox.test适用于单样本和两样本的均值检验，单样本 Wilcoxon 秩和检验，两样本 Wilcoxon 符号秩和检验

代码 
x <- c(0.80, 0.83, 1.89, 1.04, 1.45, 1.38, 1.91, 1.64, 0.73, 1.46)
y <- c(1.15, 0.88, 0.90, 0.74, 1.21)
wilcox.test(x, y, alternative = "g") # greater

    Wilcoxon rank sum exact test

data:  x and y
W = 35, p-value = 0.1272
alternative hypothesis: true location shift is greater than 0

2.3.2.2 方差检验

代码 
ansari.test(x, y)

    Ansari-Bradley test

data:  x and y
AB = 36, p-value = 0.1372
alternative hypothesis: true ratio of scales is not equal to 1
代码 
mood.test(x, y)

    Mood two-sample test of scale

data:  x and y
Z = 1.3827, p-value = 0.1668
alternative hypothesis: two.sided
代码 
# fligner.test只能用于样本量相同的
fligner.test(extra ~ group, data = sleep)

    Fligner-Killeen test of homogeneity of variances

data:  extra by group
Fligner-Killeen:med chi-squared = 0.21252, df = 1, p-value = 0.6448

2.4 多样本检验

多样本检验（也称为多组检验）是统计学中用于分析三组或更多样本均值是否存在显著差异的一类方法。

2.4.1 正态总体

2.4.1.1 均值检验

对于多样本正态总体的均值检验，最常用的方法是单因素方差分析（ANOVA），它适用于以下情况：

  • 正态性：数据应来自正态分布的总体。

  • 独立性：各组样本之间相互独立。

  • 方差齐性：各组的方差应该相等。

F分布

2.4.1.1.1 方差相同
代码 
# 假设各组方差相同
oneway.test(weight ~ group, data = PlantGrowth, var.equal = TRUE)

    One-way analysis of means

data:  weight and group
F = 4.8461, num df = 2, denom df = 27, p-value = 0.01591
2.4.1.1.2 异方差

计算各组方差

代码 
aggregate(data = PlantGrowth, weight ~ group, FUN = var)
  group    weight
1  ctrl 0.3399956
2  trt1 0.6299211
3  trt2 0.1958711

异方差情况下方差分析

代码 
oneway.test(weight ~ group, data = PlantGrowth, var.equal = FALSE)

    One-way analysis of means (not assuming equal variances)

data:  weight and group
F = 5.181, num df = 2.000, denom df = 17.128, p-value = 0.01739

2.5 配对样本检验

配对样本检验（Paired Sample Test）是一种统计检验方法，用于比较两个相关样本之间的差异。它通常用于以下情况：

  1. 重复测量：同一组对象在不同时间点或不同条件下进行测量。例如，测量同一组学生在培训前后的考试成绩。

  2. 匹配样本：在两个相关群体中进行比较，例如在临床试验中比较接受治疗前后的患者健康状况。

配对样本与独立两样本差异
  • 配对样本检验和独立两样本检验（正常的两样本检测）之间的主要区别在于样本之间的关系和数据结构。以下是它们的主要区别：

    1. 样本关系：

      • 配对样本检验：样本是相关的，通常是同一组对象在不同时间点或条件下的测量结果。例如，测量同一组患者在治疗前后的血压。

      • 独立两样本检验：样本是独立的，来自不同的群体或组别。例如，比较两组不同患者的血压，一组接受了治疗，另一组未接受治疗。

    2. 数据结构：

      • 配对样本检验：数据以配对的形式出现，每对数据之间有直接的关联。差值用于进行分析。

      • 独立两样本检验：数据来自两个不同的群体，无法通过简单的差值进行分析，通常比较两个均值或分布。

    3. 假设条件：

      • 配对样本检验：通常要求配对的差值呈正态分布（对于配对t检验），但对于Wilcoxon符号秩检验则没有正态性要求。

      • 独立两样本检验：通常要求两个样本的观察值是独立的，并且对于t检验，样本的方差可能需要相等（可以使用Welch’s t检验来放宽这一假设）。

    4. 使用场景：

      • 配对样本检验：适用于研究在干预或处理前后的变化。

      • 独立两样本检验：适用于比较两个不同组之间的差异。

配对样本检验的常见类型有：

  • 配对t检验：用于比较两个配对样本的均值，假设样本来自于正态分布。
代码 
sleep2 <- reshape(sleep,
  direction = "wide",
  idvar = "ID", timevar = "group"
)
t.test(Pair(extra.1, extra.2) ~ 1, data = sleep2)

    Paired t-test

data:  Pair(extra.1, extra.2)
t = -4.0621, df = 9, p-value = 0.002833
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -2.4598858 -0.7001142
sample estimates:
mean difference 
          -1.58
代码 
with(sleep, pairwise.t.test(x = extra, g = group, paired = TRUE))

    Pairwise comparisons using paired t tests 

data:  extra and group 

  1     
2 0.0028

P value adjustment method: holm
  • Wilcoxon符号秩检验：用于非参数数据的配对样本检验，适用于不满足正态分布假设的情况。

配对样本检验的基本思路是计算每对样本的差值，然后对这些差值进行统计分析，以判断样本之间是否存在显著差异。

3 相关知识

3.1 α、β及检验功效

在统计学中，第一类错误、第二类错误和检验功效是假设检验中的关键概念，它们描述了在进行统计推断时可能遇到的不同类型的错误和正确决策的概率。

  1. 第一类错误（Type I Error）：

    • 定义：在假设检验中，错误地拒绝了一个真实的零假设（null hypothesis, H0）。

    • 概率：第一类错误发生的概率通常用α表示，称为显著性水平（significance level）。例如，如果α设定为0.05，那么在进行100次假设检验中，平均会有5次是错误地拒绝了真实的零假设。

    • 后果：第一类错误可能导致错误的结论，如错误地认为某种药物有效，而实际上它没有效果。

  2. 第二类错误（Type II Error）：

    • 定义：在假设检验中，未能拒绝一个错误的零假设（即零假设实际上是不成立的，但检验结果未能显示这一点，错误的接受了一个错误的零假设）。

    • 概率：第二类错误发生的概率用β表示。检验功效（power）是1-β，表示正确拒绝错误零假设的概率。

    • 后果：第二类错误可能导致忽视了实际存在的效果或差异，例如，未能发现某种药物的实际疗效。

  3. 检验功效（Power of a Test）：

    • 定义：在零假设实际上是错误的情况下，检验能够正确拒绝零假设的能力或概率。

    • 计算：检验功效通常用1-β表示，其中β是犯第二类错误的概率。

    • 影响因素：检验功效受样本大小、效应大小（即实际差异或效果的大小）、显著性水平和数据的变异性等因素影响。

    • 目标：在设计实验或研究时，研究者通常希望检验功效尽可能高，以确保能够检测到实际存在的效果。通常，检验功效至少应设定为0.8（即80%）。

在实际应用中，研究者需要平衡第一类错误和第二类错误的风险，并根据研究的目的和重要性来选择合适的显著性水平和样本大小，以确保检验的功效。

3.2 样本量的确定

确定样本量通常涉及功效分析和显著性水平的设定。以下是一个简要的步骤指南：

  1. 定义研究目标：明确你要检验的假设（例如，比较两组均值）。

  2. 设定显著性水平（α）：通常设定为0.05，表示有5%的概率拒绝正确的原假设（即发生第一类错误）。

  3. 设定功效（1 - β）：功效是正确拒绝原假设的概率，通常设定为0.80或0.90，表示有80%或90%的概率检测到实际存在的效应（即发生第二类错误的概率为20%或10%）。

  4. 估计效应大小：效应大小是指你希望检测的最小差异。在比较两组均值时，效应大小可以用Cohen’s d来表示，计算公式如下：

    \[d = \frac{\bar{X_1}-\bar{X_2}}{s}\]

  • d < 0.2：小效应

  • 0.2 ≤ d < 0.5：中等效应

  • 0.5 ≤ d < 0.8：大效应

  • d ≥ 0.8：非常大的效应

计算样本量的公式为 \[n = \frac{(Z_{\alpha/2}+Z_\beta)^2·(2\sigma^2)}{d^2}\]

  • \(Z_{α/2}\)：对应显著性水平的Z值（例如，α=0.05时，Z=1.96）

  • \(Z_β\)：对应功效的Z值（例如，功效为0.80时，Z=0.84）

  • σ：总体标准差的估计

  • d：期望的效应大小（两组均值的差异）

两组比较

代码 
library(pwr)

# 设置参数
alpha <- 0.05 # 显著性水平
power <- 0.80 # 功效
d <- 0.5 # 期望的效应大小（Cohen's d）

# 计算样本量
sample_size <- pwr.t.test(d = d, power = power, sig.level = alpha, type = "two.sample")
print(sample_size)

     Two-sample t test power calculation 

              n = 63.76561
              d = 0.5
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group

多组比较

代码 
# k为分组数量
# f：效应大小，这是ANOVA中的一个重要参数，它衡量了不同组之间均值差异的标准偏差与组内标准偏差的比值。效应大小f的计算公式为：
pwr.anova.test(f = 0.28, k = 4, power = 0.80, sig.level = 0.05)

     Balanced one-way analysis of variance power calculation 

              k = 4
              n = 35.75789
              f = 0.28
      sig.level = 0.05
          power = 0.8

NOTE: n is number in each group
  1. 调整样本量：考虑到可能的缺失数据或其他因素，适当增加样本量。

3.3 随机试验的局限性

随机试验，尤其是随机对照试验（RCT），是科学研究中用于确定因果关系的重要工具。然而，尽管RCT被认为是确定干预效果的“金标准”，它们也有一些局限性：

  1. 成本高昂：RCT可能需要大量的时间和资源来设计、实施和分析。

  2. 样本代表性：由于严格的纳入和排除标准，RCT的样本可能无法代表更广泛的人群，这可能限制了研究结果的普遍适用性。

  3. 外部有效性：RCT通常在受控的环境中进行，这可能不完全反映现实世界的条件，因此结果可能难以推广到一般人群。

  4. 伦理问题：在某些情况下，如严重疾病的治疗，使用安慰剂对照可能会引发伦理上的争议。

  5. 实施难度：RCT需要高度的标准化和控制，这在实际应用中可能难以实现。

  6. 参与者的依从性：在RCT中，参与者可能不会完全遵守研究协议，这可能影响结果的准确性。

  7. 结果的普遍性：RCT的结果可能不适用于不同的人群或环境。

  8. 可能存在选择偏差：尽管随机化旨在减少偏差，但如果执行不当，仍可能存在选择偏差。

  9. 可能存在信息偏倚：如果研究设计不当，可能会产生信息偏倚，尤其是在数据收集和分析过程中。

  10. 随机化可能不充分：在某些情况下，随机化过程可能不充分，导致组间存在不均衡。

  11. 长期效果未知：RCT可能无法评估干预措施的长期效果，因为它们通常在有限的时间内进行。

  12. 干预的一致性：在RCT中，干预措施需要标准化，这可能限制了干预的灵活性和个性化。

  13. 结果的解释性：RCT的结果可能受到混杂因素的影响，使得因果关系的解释变得复杂。

  14. 数据丢失：在RCT中，可能会有数据丢失，如参与者退出研究，这可能会影响结果的可靠性。

  15. 统计功效：如果样本量计算不当，RCT可能无法检测到实际存在的效果，即统计功效不足。

了解这些局限性对于正确设计、执行和解释RCT至关重要。研究人员需要权衡RCT的优势和局限性，并考虑使用其他研究设计来补充RCT的结果。

回到顶部